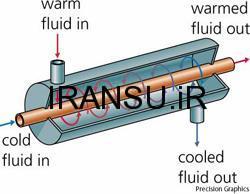
مبدل گرمایی با جریان همسو
در شکل توزیع دمای سیال گرم و سرد در مبدل گرمایی با جریان همسو ( مبدل tubular ) نشان داده شده است . اختلاف دمای ابتدا بزرگ است اما با افزایش x سریعاَ کاهش می یابد و به طور مجانبی به صفر نزدیک می شود باید توجه داشت که در چنین مبدلی دمای خروجی سیال سرد هیچ وقت از دمای خروجی گرم بیشتر نمی شود . در شکل اندیس های ۱ و ۲ دو سر متقابل را در مبدل نشان می دهد از این قرارداد برای تمام انواع مبدل های گرمایی استفاده می شود .
نمودار دما در طول مبدل برای جریان همسو و ناهمسو
طبق تعریف \dot{Q}= UA \Delta T_m که در آن U ضریب انتقال حرارت کلی مبدل و A سطح تبادل حرارت در مبدل است.همچنین با کاربرد موازنه انرژی برای عناصر دیفرانسیلی از سیالات گرم و سرد شکل {\Delta T_m} را می توان تعیین کرد البته اثبات آن در اینجا بیان نمی شود . هر عنصر دارای طول dx و مساحت سطح انتقال گرمای dA است . برای موازنه های انرژی و تحلیل پیرو آن ، فرض های زیر را در نظر می گیریم :
۱- مبدل گرمایی از اطراف خود عایق شده است ،و در این حالت تبادل گرما فقط بین سیالات گرم و سرد است .
۲- رسانش محوری در امتداد لوله ها ناچیز است .
۳- تغییرات انرژی پتانسیل و جنبشی ناچیز است .
۴- گرماهای ویژه سیالات ثابت اند .
۵- ضریب کلی انتقال گرما ثابت است .
البته گرماهای ویژه بر اثر تغییرات دما تغییر می کنند ، و ضریب کلی انتقال گرما بر اثر تغییرات خواص سیال و شرایط جریان ممکن است تغییر کند . ولی ، در بسیاری از کاربردها این تغییرات خواص قابل توجهی نیستند و می توان با مقادیر متوسط cpc ,، cph ,h و U کار کرد. برای بدست آوردن U داریم.
\frac {1} {A}U_{pre} = \Sigma \frac{1} {hA} + \Sigma R
\frac{1}{U_{exp}} = \frac{1}{U_{pre}}+R_f
R = مقاومت گرمایی دیواره لوله ها
h = ضریب انتقال حرارت سیال ( سیال گرم و سیال سرد) که از روابط تئوری و تجربی بدست می آید. بسته به این که تغییر فاز داشته باشیم یا نداشته باشیم و هندسه انتقال حرارت . روابطی برای محاسبه آن در کتابهای انتقال حرارت موجود است.
U_{exp}=ضریب انتقال حرارت کلی برای مبدل با محاسبه تاثیر رسوبات
U_{pre}=ضریب انتقال حرارت بر مبنای تمیز بودن(بدون رسوب) مبدل
R_f=مقاومت گرمایی لوله ها بر اثر رسوب
که معمولا از R ( مقاومت گرمایی لوله ها) صرف نظر میکنیم . در نهایت برای جریان همسو داریم.
\Delta {T_m}=\frac{\Delta T_1-\Delta T_2}{\ln \left( \frac{\Delta T_1}{\Delta T_2}\right) }
\Delta T_1 = T_{h1} – T_{c1}
\Delta T_1 = T_{h2} – T_{c2}
Heat exchanger with parallel flow
In the distribution of hot and cold fluid temperatures in the heat exchanger with parallel flow (ADC tubular) are shown.. In the indices 1 and 2 show both the mutual conversion
The contracts for all types of heat exchangers are used.
Temperature profile along the line and Countercurrent Flow Converters
By definition, \ dot {Q} = UA \ Delta T_m where the overall heat transfer coefficient U and A-level converters also heat exchangers using the energy balance for a differential element of the hot and cold fluids {\ Delta T_m} to can be determined, of course, prove that it is not described here. Each element of length dx and dA is the surface area of heat transfer. Energy balance analysis to follow, we consider the following assumptions:
1 heat exchanger is insulated from its surroundings, and in this case only the heat exchange between the hot and cold fluids.
2 axial conduction along the tubes is negligible.
3 Kinetic and potential energy changes are negligible.
4 Special Fluid Grmahay fixed.
5 The heat transfer coefficient is constant.
The Special Grmahay of temperature change, and heat transfer coefficient due to changes in fluid properties and flow conditions may change. However, in many applications, these changes are not significant benefits can be achieved with moderate amounts cpc ,, cph, h and U worked. U have to get.
\ frac {1} {A} U_ {pre} = \ Sigma \ frac {1} {hA} + \ Sigma R
\ frac {1} {U_ {exp}} = \ frac {1} {U_ {pre}} + R_f
R = thermal resistance of the tube wall
h = coefficient of heat transfer fluid (hot fluid and cold fluid) that the relationship between theory and experiment is obtained. Depending on whether or not we have a phase change heat transfer and geometry. Equations for the calculation of heat transfer in the books available.
U_ {exp} = overall heat transfer coefficient is calculated by converting the effect of sediment
U_ {pre} = heat transfer coefficient based on being clean (no deposit) Converter
R_f = thermal resistance due to fouling of pipes
Usually the R (resistance heat pipes) are ignored. Finally we get to the line.
\ Delta {T_m} = \ frac {\ Delta T_1- \ Delta T_2} {\ ln \ left (\ frac {\ Delta T_1} {\ Delta T_2} \ right)}
\ Delta T_1 = T_ {h1} – T_ {c1}
\ Delta T_1 = T_ {h2} – T_ {c2}
Hrarty, ADC testing testing testing Mtqat, flow heat exchanger heat exchanger heat exchanger tubes Ay, water, water to water heat exchanger Grm, Hva, heat exchanger water heat exchanger hot water heater Dyvary, Msrfy, heat exchanger heat exchanger Lfalaval, Lvlh, thermal shell heat exchanger with parallel flow